Smart HPC

Complex HPC applications typically rely on libraries to provide a number of numerical methods for solving specific subproblems, such as solving large, sparse systems of linear equations, computing eigenvalues and eigenvectors, and many other numerical types of numerical computations. Many new algorithms and multiple implementaions of existing algorithms are continously being developed by the applied mathematics and computational science researchers. The accuracy and performance of different solution approaches generally depends on the characteristics of the problem being solved; in complex application, it is often impossible to theoretically determine which algorithm would be the best for a given set of inputs. We are developing methodologies and software infrastructure that can analyze algorithms and their implementation to aid HPC application developers in the selection and effective use of the ever-growing wealth of existing numerical software.

For example, we perform research on multimethod linear solvers, i.e., solvers that combine more than one underlying algorithm to improve the performance of large-scale simulations. In the past we have developed adaptive solvers, which use heuristics to select a solution method to better match the changing attributes of linear systems generated in different stages of an application. We have also developed composite solvers, which use a sequence of methods on the same linear system to improve reliability.

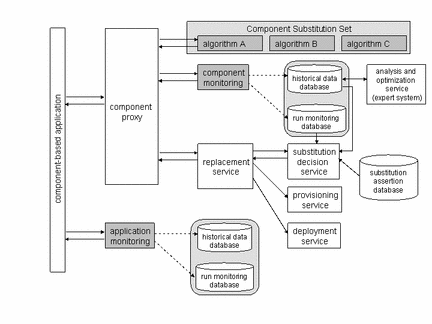
The diagram to the right illustrates an example runtime scenario of the components involved in multimethod linear system solution, which is a part of an application, such as the solution of a nonlinear PDE. We have demostrated the effectiveness of composite and adaptive linear solver techniques in a number of applications, such as a driven cavity flow simulation, and simulation of flow around an airfoil.